■ 回転補正について
多くのスマートフォンは重力加速度センサと地磁気(方位)センサを搭載しているため,それらを利用してデバイスの向き(姿勢)を表す3つの角度(オイラー角)を算出できる.以下では,測定したオイラー角を用いて,デバイスに固定された座標系での加速度を静止座標系での加速度に変換できることを説明する.
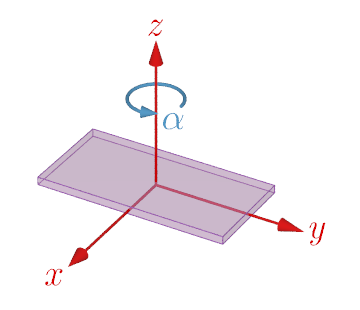
$z$軸周りの回転
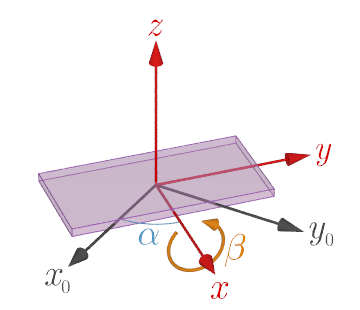
$x$軸周りの回転
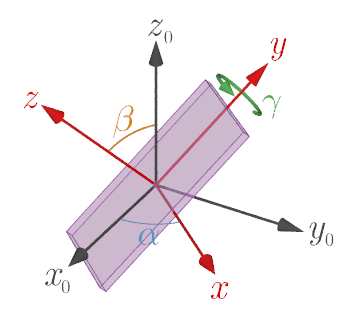
$y$軸周りの回転
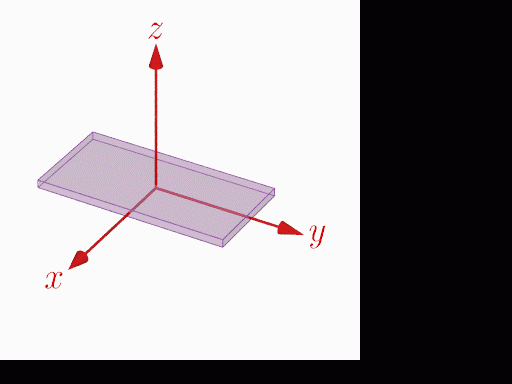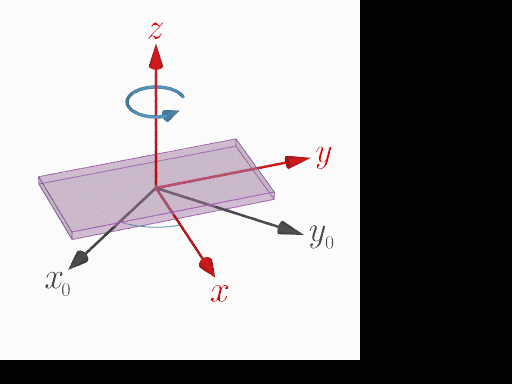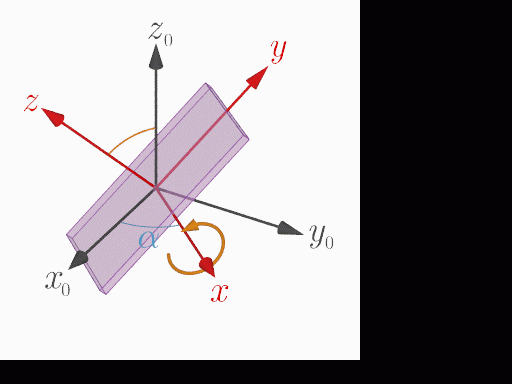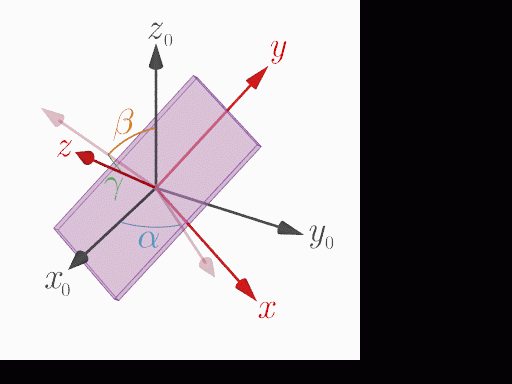
本サイトの加速度測定アプリはWebブラウザ上で動作するWebアプリであり JavaScript で作られている.Webブラウザではデバイスの姿勢情報(オイラー角)と加速度を検出するために,それぞれ,DeviceOrientationEvent と DeviceMotionEvent というAPIが用意されている.このAPIで取得できるオイラー角 $\alpha$, $\beta$, $\gamma$ は,この順番でデバイスに固定された座標系の$z$, $x$, $y$ 軸周りに回転する角度($z$-$x$-$y$系のオイラー角)を表している(乗り物やロボットなどでよく用いられるロール・ピッチ・ヨー角($z$-$y$-$x$系のオイラー角)とは異なる).
加速度の測定と共に時々刻々のオイラー角を測定すると,測定開始時の静止座標系を基準として,デバイスがどれだけ回転しているかが分かる.オイラー角 $\alpha$, $\beta$, $\gamma$ についての回転行列 $R_z(\alpha)$, $R_x(\beta)$, $R_y(\gamma)$ は次式で与えられる:
$$ \tag{1} R_z(\alpha)=\begin{pmatrix} \cos\alpha & -\sin\alpha & 0 \\ \sin\alpha & \cos\alpha & 0 \\ 0 & 0 & 1 \end{pmatrix} $$ $$ \tag{2} R_x(\beta)=\begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\beta & -\sin\beta \\ 0 & \sin\beta & \cos\beta \end{pmatrix} $$ $$ \tag{3} R_y(\gamma)=\begin{pmatrix} \cos\gamma & 0 & \sin\gamma \\ 0 & 1 & 0 \\ -\sin\gamma & 0 & \cos\gamma \\ \end{pmatrix} $$
ここで,静止座標系で成分表示されたベクトル $\boldsymbol{a}_0=\left(a_{0x},\,a_{0y},\,a_{0z}\right)$ から,$z$-$x$-$y$系のオイラー角により回転変換された座標系での成分表示 $\boldsymbol{a}=\left(a_{x},\,a_{y},\,a_{z}\right)$ を得ること(座標変換)を考える.この場合,$\boldsymbol{a}_0$ を$z$軸周りに角$\alpha$だけ逆回転させ,次に$x$軸周りに角$\beta$だけ逆回転,さらに$y$軸周りに角$\gamma$だけ逆回転させればよいので
$$ \tag{4} \begin{aligned} \boldsymbol{a}&=R_y^{-1}(\gamma)R_x^{-1}(\beta)R_z^{-1}(\alpha)\boldsymbol{a}_0 \\ &=\left\lbrace R_z(\alpha)R_x(\beta)R_y(\gamma)\right\rbrace^{-1}\boldsymbol{a}_0 \end{aligned} $$と表せる.よって,$\boldsymbol{a}$ から $\boldsymbol{a}_0$ を得るには式(4)の逆変換を考えればよく,デバイス固定の座標系で測定された加速度 $\boldsymbol{a}$ は変換行列
$$ \tag{5} M=R_z(\alpha)R_x(\beta)R_y(\gamma) $$を用いて,静止座標系での加速度
$$ \tag{6} \boldsymbol{a}_0=M\boldsymbol{a} $$に変換できるというわけである.
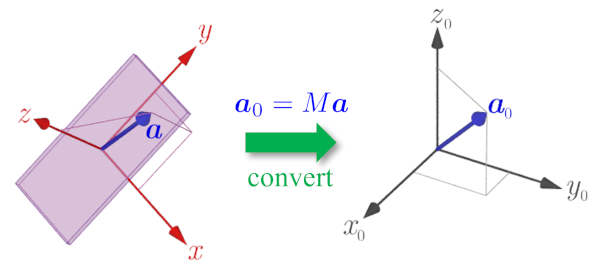
デバイス固定の座標系から静止座標系への変換