【操作方法】
■ 最小二乗近似によるデータの平滑化
本アプリでは,データの平滑化(ノイズ除去)の方法として,フーリエ変換による方法と最小二乗近似による方法を用意している.
ここでは,例として,下図のような加速度データが得られたとして,最小二乗近似を用いて平滑化 1) する方法を説明する.
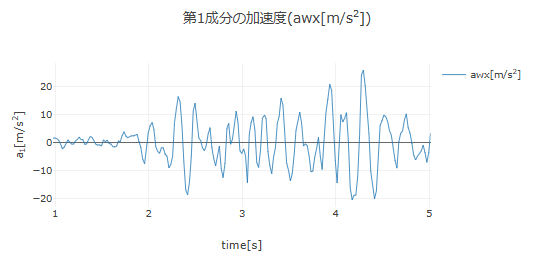
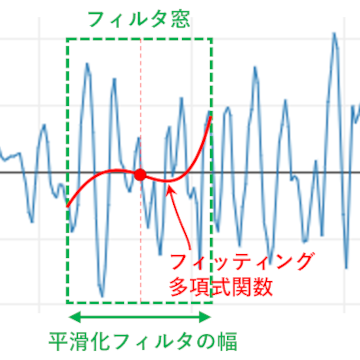
最小二乗近似による平滑化では,平滑化フィルタ窓内にあるデータに対して,最小二乗法を用いて多項式関数でフィッティングし,フィルタ幅の中央における関数値をその点の平滑化されたデータの値とする.フィルタ窓をデータの左端から右端にずらしていきながら,同様のフィッティングを行って,平滑化されたデータを得る.この方法は,測定データの時間刻み幅が常に一定であれば,Savitzky-Golay平滑化 2) と同じである.
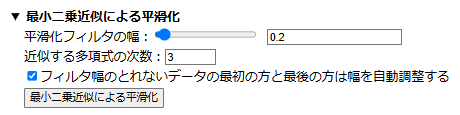
加速度データを読み込み,「分析に使用する時間領域の設定」を行うと,加速度データのグラフが表示され,その下に「加速度データの平滑化」のエリアが現れる.「▶ 最小二乗近似による平滑化」の行をクリックすると,最小二乗近似の設定欄が現れる.平滑フィルタの幅をスライダーもしくは数値の入力により設定し,近似する多項式の次数を入力する.データの両端はフィルタ幅がとれないので,自動調整するにチェックを入れておく(チェックを外すと両端が元データからずれる).設定後,「最小二乗近似による平滑化」ボタンを押すと,平滑化された加速度のグラフが,元の加速度のグラフに重ねて,下図のように表示される(平滑フィルタ幅を0.2,近似する多項式の次数を3に設定).

ここで,オレンジ線(smth_awx)が平滑化されたデータであり,緑線(diff_awx)は差分データ(元のデータから平滑化されたデータを引いたもの)を示す.平滑化されたデータのグラフ(オレンジ線)を見ると,細かい振動成分(ノイズ)が元のデータから除去されていることが分かる.
多項式の次数は3のまま変えずに平滑化フィルタの幅を0.5,1.0と増やした場合のグラフを順に以下に示す.急激に変化しているデータに対してフィルタ幅をあまり大きくすると,次数の低い多項式では近似できないことが分かる.

平滑フィルタ幅1.0,多項式の次数3の場合の平滑化

また,平滑化フィルタの幅を0.2,多項式の次数を0にした場合のグラフを以下に示す.次数が0の多項式とは定数のことであり,この場合,定数の値はフィルタ窓内のデータの平均値となる.


加速度データの平滑化を行うと,「数値積分する加速度データの選択」の欄が現れ,速度を求めるために数値積分する加速度として,「元のデータ」「平滑化データ」「差分データ」のいずれかを選択できるようになる.また,「平滑化のクリア」ボタンを押すと平滑化データと差分データのグラフを消去する.
速度や位置のデータについても,最小二乗近似による平滑化を同様に行うことができる.
【参照】
- Peter A. Gorry, General Least-Squares Smoothing and Differentiation of Nonuniformly Spaced Data by the Convolution Method, Analytical Chemistry 63, 534-536 (1991).
- Abraham. Savitzky and M. J. E. Golay, Smoothing And differentiation of Data by Simplified Least Squares Procedures, Analytical Chemistry 36, 1627-1639 (1964).